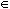A and bi 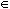B}.
Since the problem involves two
input integer Sets, we declare them as
Set<int>:
|
|
To illustrate the basics, let's write a program to compute and display the
Cartesian product of two integer Sets.
The Cartesian product of two sets, A and
B, is the set of all possible pairs
of elements from
A and B.
More
formally, if A = {a1,...,an} and B
= {b1, ...,bn}, then A[times ]B = {<ai,bi> | ai
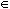A and bi 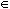B}.
Since the problem involves two
input integer Sets, we declare them as
Set<int>:
#include <Set.h>
Set<int> a, b; declares a and b as Set<int>
Since it generates as a result a Set of integer pairs, we first define a type Pair and then use it to declare the result as Set<Pair>:
struct Pair{
int i;
int j;
};
Set<Pair> result; illegal!
As noted, this is incorrect;
Set(C++)
specifies
that any type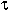 
used as an argument to Set<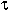> must
meet three requirements:
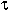must have a parameterless constructor ()
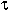must have a copy constructor (&)
must have an operator== defining an equivalence
relation on .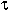
struct Pair{
int i;
int j;
};
int operator==(const Pair& p1,const Pair& p2){
return p1.i==p2.i && p1.j==p2.j;
}
Set<Pair> result; OK
Since the problem states that we must display the answer, we will need a stream insertion operator for Set<Pair>. Set(C++) explains that in order to do this, Pair must itself have a stream insertion operator. We must therefore write one:
#include <iostream.h>
ostream& operator<<(ostream& os,const Pair& p){
os << "<" << p.i << "," << p.j << ">";
return os;
}
We are now ready to implement the Cartesian product function, which we define by overloading the multiplication operator:
Set<Pair> operator*(const Set<int>& a,
const Set<int>& b){
Set<Pair> result;
Setiter<int> a_iter(a);
const int* ap;
while(ap = a_iter.next()){
Pair p;
p.i = *ap;
Setiter<int> b_iter(b);
const int* bp;
while(bp = b_iter.next()){
p.j = *bp;
result.insert(p);
}
}
return result;
}
The operator takes two constant integer Set references a and b (avoiding copy), and returns a Set of integer pairs result (requiring a copy). It creates the result by looping over the elements of a and, for each element, looping over the elements of b and forming the Pair <ai,bj>, which it inserts into result. As for other container classes, iteration over Sets is done by creating an iterator (for example, Setiter<int> a_iter(a)) and then repeatedly requesting the ``next'' element from the iterator until the iterator returns zero. Set, Bag, and pointer set iterators return pointers; this avoids a copy and, since the pointers are to constant objects, prevents the client from modifying elements. The main program will test the function by computing the Cartesian product {1,2,3,4}[times ]{5,6}:
main(){
Set<int> s(1,2,3,4), t(5,6);
cout << s*t << "\ n";
}
We can now compile our program, which we assume to be in a single file called cartesian.c. For Sets, instead of using the default hash function, we can provide our own hash functions for integers and Pairs, respectively. A hash function must take an argument of the Set element type, compute an integral value from it, preferably unique, and then return the unsigned integral type Set_or_Bag_hashval, which for UnixWare and most other implementations is unsigned long, but might be different on some machines. See Set(C++). This value is used by the Set operations to determine an element's location within the Set's internal data structure. If you provide a perfect hash function (one that returns different results for different arguments), execution speed will be optimized since each element will have a unique location in the data structure. So unless you are willing to pay for linear time complexity, you should provide a hash function for your element type. The section, ``Space-time tradeoffs'', discusses this subject further and gives a concrete example.
Returning to our example, here are our two hash functions:
Set_or_Bag_hashval Set<int>::hash(const int& i){
return ((Set_or_Bag_hashval)i);
}
Set_or_Bag_hashval Set<Pair>::hash(const Pair& p){
return ((Set_or_Bag_hashval)
(Set<int>::hash(p.i)+Set<int>::hash(p.j)));
}
Note that the integer hash function Set<int>::hash will be perfect as long as the type Set_or_Bag_hashval has more bits than int. The Pair hash function Set<Pair>::hash is not perfect since <i,j> and <j,i> hash to the same value.
We can now compile and link the program:
$CC cartesian.c -l++
Executing the program for the given data produces the following output:
{<1,5>,<1,6>,<2,5>,<2,6>,<3,5>,<3,6>,<4,5>,<4,6>}
After testing the function more thoroughly, we might decide to place it in a library, possibly with other functions for operating on Sets of Pairs. This will require tearing apart cartesian.c and creating a more appropriate source structure. As always when working with template classes, the class declaration should be created in the argument declaration file:
Set_Pair.h
#include <Set.h>
struct Pair{
int i;
int j;
};
int operator==(const Pair& p1,const Pair& p2){
return p1.i==p2.i && p1.j==p2.j;
}
relation.h
#include "Set_Pair.h"
Set<Pair> operator*(const Set<int>& a,
const Set<int>& b);
declarations for other useful functions involving relations
relation.c #include "relation.h"
Set<Pair> operator*(const Set<int>& a,
const Set<int>& b){
...
}
other definitions
implement.c #include "Set_Pair.h"
Set_or_Bag_hashval Set<int>::hash(const int& i){
return ((Set_or_Bag_hashval)i);
}
Set_or_Bag_hashval Set<Pair>::hash(const Pair& p){
return ((Set_or_Bag_hashval)
(Set<int>::hash(p.i)+Set<int>::hash(p.j)));
}
... other implementations
Assuming relation.c and implement.c have been compiled and placed in a library archive libRel.a, a client program would look like this:
client.c #include "relation.h"
main(){
Set<int> s(1,2,3,4), t(5,6);
cout << s*t << "\ n";
}
and would be compiled and linked as follows:
$CC client.c libRel.a -l++