A Simple Finite State Acceptor

A finite state acceptor is a finite state machine with no outputs. The user of a finite state acceptor caresonly about the final state: if the machine ends in an accepting state after processing a series of inputs, the machine is said to have accepted the input; otherwise, it is said to have rejected the input.

A common application of finite state acceptors is checking a character string for conformance with a regular expression.

Our goal in this section is to write a function called check_string() that checks a string using an Fsm that has previously been programmed to accept sequences of characters conforming to some regular expression. (For an easier way of checking whether a string matches a regular expression, see Regex(C++)).

       int check_string(char* p,Fsm& a){
           //  Check string p using Fsm a.
           //  Return 1 if the string is accepted by a.
           //  Return 0 otherwise.
       }

Suppose the following regular expression is to be used for checking:

       [0-9]*[A-Z][a-z0-9]*

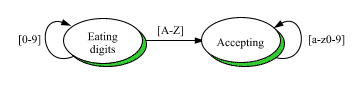
Our first task is to program a machine. Because there is no constructor taking a regular expression directly, the problem will be solved by (1) hand-translating the regular expression to a state transition diagram and then (2) `programming' the machine directly from the diagram. Figure 2 shows the state transition diagram that we will use:

Acceptor State Transition Diagram

Note that the output portion of each label has been omitted; this is consistent with the fact that acceptors don't produce output. We have also taken the liberty of labeling the input portion of each arc with the terms of the regular expression rather than drawing several arcs, each with a distinct input. This shorthand permits one arc to stand for many arcs, thereby simplifying the diagram. As we will see below, this shorthand is also recognized by function trans().

Figure 2 shows only two states, which it labels symbolically. As can be seen by the following enumeration type, however, our intent is to define a machine with three states:

       enum States{rejecting,eating_digits,accepting};

The state not shown in the diagram (rejecting) is the one the machine will enter upon receipt of an input for which no transition has been explicitly defined (recall the behavior of an unprogrammed machine in ``A Simple Vending Machine'').

If the machine enters this state, we will know that a bad character has been encountered. We must also consider the possibility that the input is exhausted before the machine reaches the ``accepting'' state; consider the input ``57''.

Since acceptors don't produce any output, they don't need action routines; we therefore omit all action routine arguments, which default to zero:

       Fsm a(3,eating_digits);  // "a" for "acceptor"
       for(int c='0';c<='9';c++){
           a.trans(eating_digits,c,eating_digits);
           a.trans(accepting,c,accepting);
       }
       for(int c='A';c<='Z';c++){
           a.trans(eating_digits,c,accepting);
       }
       .
       .

These loops, which are tedious to write and hard to understand, can be eliminated by using a second version of trans(), which takes a range of integers and creates a transition for each value in the range:

       a.trans(eating_digits,'0','9',eating_digits);
       a.trans(eating_digits,'A','Z',accepting);
       a.trans(accepting,'a','z',accepting);
       a.trans(accepting,'0','9',accepting);

Unfortunately, this code is only slightly better. A third version of trans() allows inputs to be defined by one-character regular expressions; it is convenient when working with inputs representing printable characters, as in this example:

       a.trans(eating_digits,"[0-9]",eating_digits);
       a.trans(eating_digits,"[A-Z]",accepting);
       a.trans(accepting,"[a-z0-9]",accepting);

We are now ready to write check_string():

       int check_string(char* p,Fsm& a){
           while(*p!=0){
               a.fire(*p++);
               if(a.state()==rejecting)return 0;
           }
           return a.state()==accepting;
       }

There is a serious flaw in check_string(): the function will only work the first time it is called! The reason for this is that the function leaves the machine in one of three possible final states; the machine needs to be reset to the proper initial state (eating_digits) for the function to work properly on subsequent calls. This can be accomplished in either of two ways. Calling function go() forces a machine into an explicit state:

       int check_string(char* p,Fsm& a){
           a.go(eating_digits);
           ...
       }

Calling function reset() causes the machine to return to the state defined as the initial state in the constructor call:

       int check_string(char* p,Fsm& a){
           a.reset();
           ...
       }